Analysis On Ed25519 Use Risks: Your Wallet Private Key Can Be Stolen

06/17/2022

By Max

Recently, security issues on Ed25519 signature libraries have come into the spotlight. For details, please refer to https://github.com/MystenLabs/ed25519-unsafe-libs.

In brief, due to some library designs being ill-considered and misuse of libraries' APIs, the attackers may extract the private key with two different signatures for the same message.

For the ins and outs of this security issue, this article will give you a comprehensive and easy-to-understand analysis.

Why Use Ed25519 to Sign?

American German cryptologist, Daniel J. Bernstein, along with other experts designed the Ed25519, the Elliptic Curve Signature Algorithm based on the 25519 series of elliptic curves. In 2005, Daniel himself proposed the 25519 series of elliptic curves for the first time.

Advantages of Ed25519

More Open: Compared to NIST Elliptic Curves, the choosing for every parameter of the 25519 series of elliptic curves is totally open and transparent, with no more doubts.
More Secure: The 25519 series of elliptic curves are specially designed which minimize the error probability to have higher security. Eg. any 32-digit random number is a valid X25519 public key that avoids any malicious data attacks.
Faster Speed: The 25519 series of elliptic curves are currently the elliptic curves with the fastest computing.

From the above strengths, more and more blockchains choose Ed25519 to be the signature algorithm.

One Image Tells Ed25519 Signature Principle

As shown above, the image has clearly shown the signature principle of Ed25519, including almost all details. If you want to have a better understanding of Ed25519, the image is for your perusal. And, from the above image, I think you can already feel that the design of Ed25519 is more complicated than the common ECDSA signature algorithm that these two vary a lot.

Ed25519 Signature Formulation

Let me introduce another algorithm that is related to Ed25519 — Schnoor Signature Algorithm. If you have come across with Schnorr Signature Algorithm, you can feel familiar with Ed25519.

Ed25519 can be deemed a variant of Schnorr. There are 2 major differences between them:

Ed25519 can use deterministic random numbers multiple times, and even adjust its private key design for this feature
Ed25519 can replace the elliptic curve from the common Short Elliptic Curve Secp256k1/Secp256r1 etc. to the Twisted Edwards Curve Ed25519.

Let's see the architecture of Schnorr to illustrate Ed25519 mathematical logic in the form of Schnorr.

To summarize the above image, Ed25519 can be defined as below:

$Setup$

$G$ is base point of elliptic curve group
$q$ is the order of elliptic curve group

$Sign(k, m)$ ：

Step 1: $x = f_1(k)$
Step 2: $A = xG$
Step 3: $r = f_2(k, m)$
Step 4: $e = f_3(R, A, m)$
Step 5: $R = rG$
Step 6: $S = r + e x \mod q$
Step 7: $Return \space (R, S)$

Therein

$k$ is private key
$m$ is the message pending to be signed
$A$ is public key
$f_1$ is a function to compute the public key $A$ according to the private key $k$
$f_2$ is a function to compute the private deterministic random number $r$ according to the private key $k$ and message $m$
$f_3$ is a function to compute the public deterministic random number $e$ according to $R$ , the public key $A$ and message $m$

Note

The above three functions $f_1$ , $f_2$ , $f_3$ can be derivated as shown in the above image. You can derivate the formulations and I won't do a prolonged explanation on this.

There is no problem with the above algorithms.

Then, what is the problem?

Engineering implementation.

Algorithm Engineering Implementation & Private Key Extract Attacking

Variant Implementation of Ed25519 Signature

Actually, when many algorithm libraries do the Ed25519 Signature Algorithm implementation, they won't really strictly follow the above image shown to implement. For efficiency and convenience, the public key $A$ generally won't be re-computed but to be temporarily stored. When signing, the public key $A$ , as one existing value, is directly used for signature computing, as shown below.

$Setup$

$G$ is base point of elliptic curve group
$q$ is the order of elliptic curve group

$Sign(k, m, A)$ ：

Step 1: $x = f_1(k)$
Step 2: $r = f_2(k, m)$
Step 3: $e = f_3(R, A, m)$
Step 4: $R = rG$
Step 5: $S = r + e x \mod q$
Step 6: $Return \space (R, S)$

And, the definitions of $k$ , $A$ , $f_1$ , $f_2$ , $f_3$ stay the same.

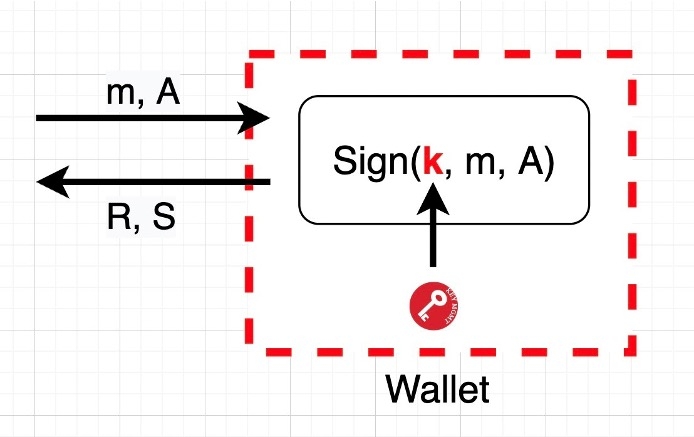
Wallet Architecture

The above image presents a common wallet architecture, including mobile wallet, hardware wallet, cloud wallet (run on a server), etc. scenarios. In the wallet architecture, the private key is generally stored in a safe place which can not be accessed by outside but can participate in signature computing.

Private Key Extract Attacking

Then how the attacking starts? Only need to attack when two signatures are initiated, and to use different public keys (such as use $A$ and $A'$ ) separately to sign.

First Signature

The attacker enters $A$ and $m$ , and the wallet enters $k$

$\Rightarrow e = f_3(R, A, m)$

$\Rightarrow S = r + ex \mod q$

Second Signature

The attacker enters $A'$ and $m$ , and the wallet enters $k$

$\Rightarrow e' = f_3(R, A’, m)$

$\Rightarrow S' = r + e'x \mod q$

As $R$ , $A$ , $A'$ , $m$ , $S$ and $S'$ are all public, so $e$ and $e'$ are also public, $S$ minus $S'$

$S-S'=(r+ex)-(r+e'x) \mod q$

$=ex-e'x \mod q$

$=(e-e')x \mod q$

And both multiplied by the inverse of $(e-e')$

$x = (S - S')(e - e')^{-1} \mod q$

Then, the $x$ is extracted.

What needs to be stressed is that we don't need extract 100% private key $k$ . Once the $x$ is extracted, then we can sign any message. That's to say, from the perspective of digital asset security, only extract $x$ equals to get the wallet private key which also means get the assets in the wallet.

Attacking Scope and Corresponding Solution

No matter what kind of wallets, whether mobile, cloud or hardware, as long as you design the Ed25519 Signature Algorithm, that is to provide interfaces similiar to $Sign(k, m, A)$ , and do not verify the public key $A$ , then it's possible to be attacked.

BTW, this attacking also can attack Schnorr.

Solutions are quite simple actually and can be divided into 2 kinds:

Do not provide interfaces similar to $Sign(k, m, A)$ . Instead, provide interfaces similar to $Sign(k, m)$ . Compute $A$ via the private key $k$ to avoid invalid entering.
If you have to provide interfaces similar to $Sign(k, m, A)$ , you must verify $A == xG$ , to make sure that the public key you enter is the only valid one.

Though the attacking is practical, we don't need to worry too much about its threat. In most scenarios, $Sign(k,m,A)$ can only be called by the user self, not the third party (potential attacking party), and the public key $A$ is also valid. So, don't be too anxious about the private key extract attacking. If $Sign(k, m, A)$ is called by a third party, then you should be cautious about this attack.

Further Thoughts on This Attacking

What's the idea behind this attack? I think you can see that in Ed25519 and Schnorr, deterministic random numbers are used multiple times which actually can tell what's the origin for this attacking.

It's not to say that using deterministic random numbers is wrong. Rather, when all parameters in a signature system are deterministic, the system is secure. Even compared to a random signature system, the former has some safer features, like always generating the same signature for the same message. However, when part of deterministic random numbers have been compromised (typically caused by engineering implementation and use ill-considered), that's where the nightmare prevails. The residual deterministic random numbers can no longer guarantee security, and even can be exploited by the attacker who via duplicate signatures eliminates deterministic invariants to attack the whole system. The attacking towards Ed25519 and Schnorr signature algorithms can partially prove this thought.

So, to guard against this hacking, we can have a new solution, that is, use "real" random numbers to completely replace the deterministic random numbers, which is to eliminate deterministic factors to circumvent such duplicate-signature-depended private key extract attacking. I will introduce the specific application of this new solution sometime in the future.

Also, one good news I want to share is that Safeheron is going to open source our MPC-related algorithms. Welcome all to take a look and we look forward to have any feedback!